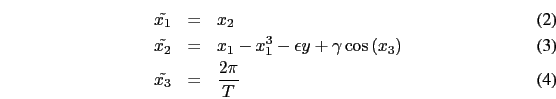duffing_diagr

Scicos Diagram
fr - eng

Duffing's oscillator

$\epsfig{file=duffing_diagr.eps,height=12cm}$

Module

Modnum

Duffing's oscillator

Description

The Duffing's equation is described by this nonlinear differential equation :

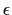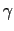$\begin{eqnarray} \frac{y\left(t\right)}{dt}&=&x\left(t\right)-x^{3}\left(t\right)-\epsilon y\left(t\right)+\gamma\cos\left(\omega t\right) \end{eqnarray}$

where $\epsilon$ and $\gamma$ are parameters and $\omega$ a pulsation.
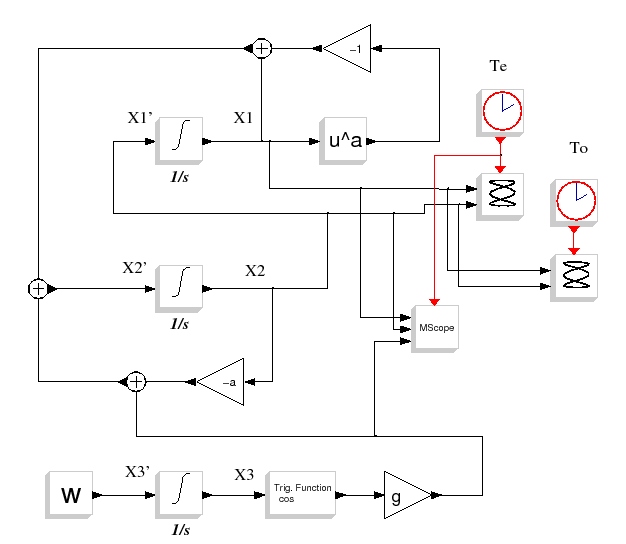
This forced oscillator should be written as a three dimensional state equation system :

$\begin{eqnarray} \tilde{x_{1}}&=&x_{2}\\ \tilde{x_{2}}&=&x_{1}-x_{1}^{3}-\epsilon y+\gamma\cos\left(x_{3}\right)\\ \tilde{x_{3}}&=&\frac{2\pi}{T} \end{eqnarray}$

Context

Te=0.02
Tfin=200
g=0.3
a=0.15
w=1
To=2*%pi/w
ci1=0.1
ci2=0.1
ci3=0

Scope Results

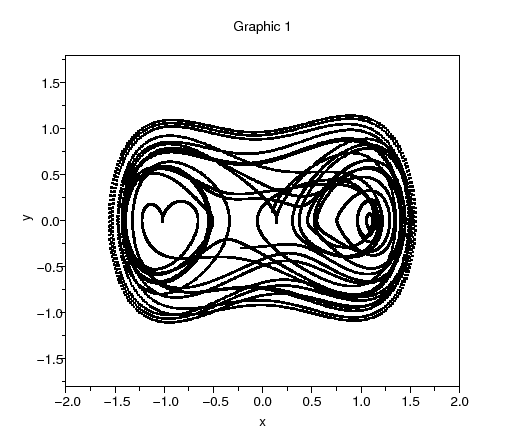
$\begin{figure}\begin{center} \epsfig{file=duffing_scope_1.eps,width=330.00pt} \end{center}\end{figure}$

Figure : (a) Phase plan

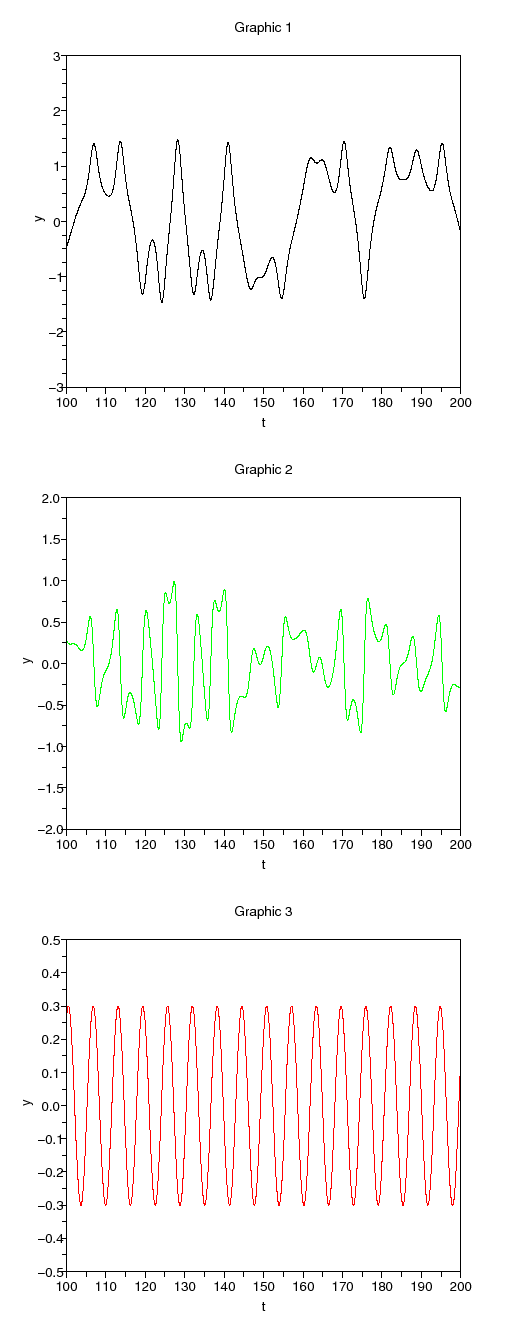
$\begin{figure}\begin{center} \epsfig{file=duffing_scope_2.eps,width=330.00pt} \end{center}\end{figure}$

Figure : (b) Time domain waveforms

$\begin{figure}\begin{center} \epsfig{file=duffing_scope_3.eps,width=330.00pt} \end{center}\end{figure}$

Figure : (c) Poincare section

Authors