Diagramme Scicos
fr - eng


Oscillateur de Duffing

\epsfig{file=duffing_diagr.eps,height=12cm}

Module


Contenu

Description

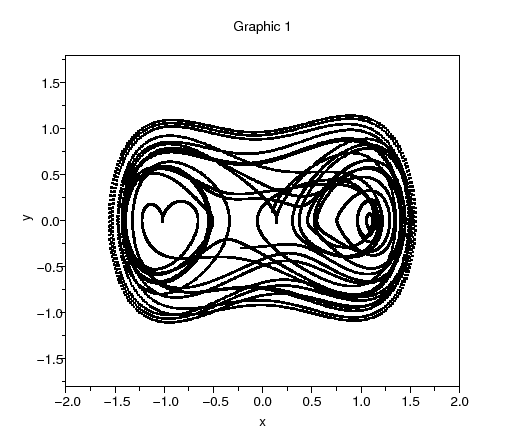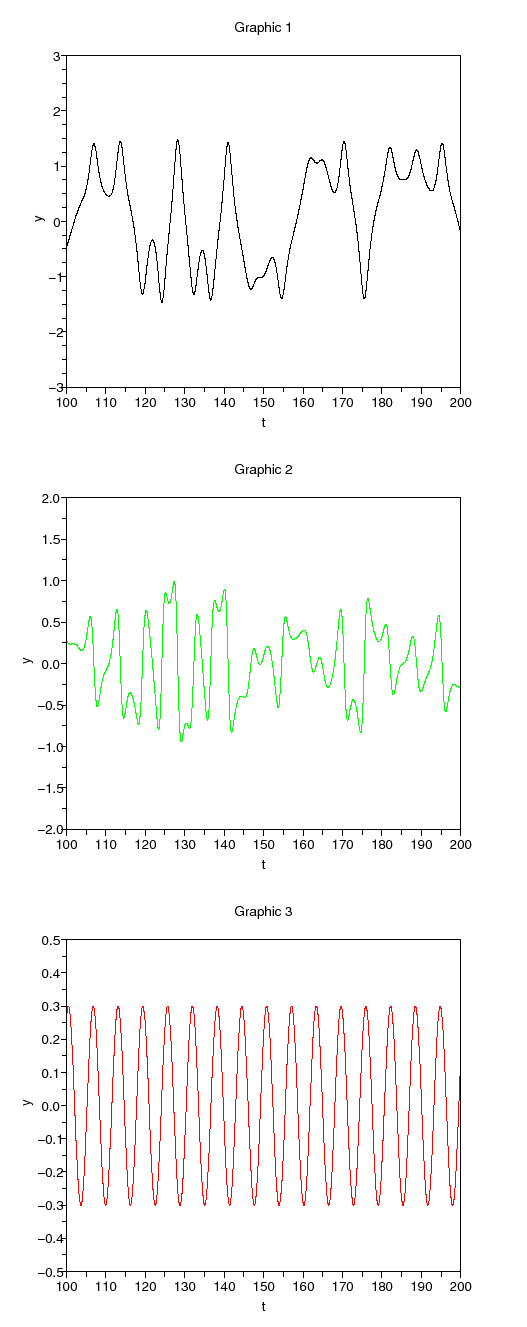
L'équation de Duffing est décrite par cette équation différentielle non-linéaire :

\begin{eqnarray} \frac{y\left(t\right)}{dt}&=&x\left(t\right)-x^{3}\left(t\right)-\epsilon y\left(t\right)+\gamma\cos\left(\omega t\right) \end{eqnarray}


où $ \epsilon$ et $ \gamma$ sont des paramètres et $ \omega$ une pulsation.

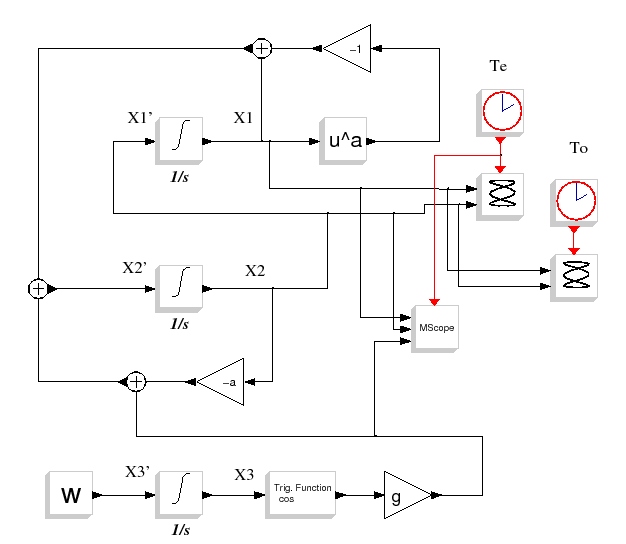
Cet oscillateur forcé peut-être écrit comme un système d'équations d'état à trois dimensions :

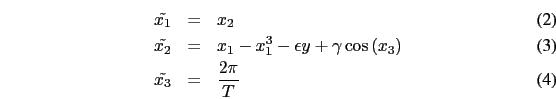
\begin{eqnarray} \tilde{x_{1}}&=&x_{2}\\ \tilde{x_{2}}&=&x_{1}-x_{1}^{3}-\epsilon y+\gamma\cos\left(x_{3}\right)\\ \tilde{x_{3}}&=&\frac{2\pi}{T} \end{eqnarray}


Contexte 


Te=0.02
Tfin=200
g=0.3
a=0.15
w=1
To=2*%pi/w
ci1=0.1
ci2=0.1
ci3=0

Résultats des oscilloscopes

\begin{figure}\begin{center} \epsfig{file=duffing_scope_1.eps,width=330.00pt} \end{center}\end{figure}
Figure : (a) Trajectoires
\begin{figure}\begin{center} \epsfig{file=duffing_scope_2.eps,width=330.00pt} \end{center}\end{figure}
Figure : (b) Formes temporelles
\begin{figure}\begin{center} \epsfig{file=duffing_scope_3.eps,width=330.00pt} \end{center}\end{figure}
Figure : (c) Section de Poincaré

Auteurs

IRCOM Group Alan Layec