dsm_gauss

Scilab simulation Script
fr - eng

Output spectra of Delta-Sigma modulator

Output spectra of Delta-Sigma modulator

Module

Modnum

Description

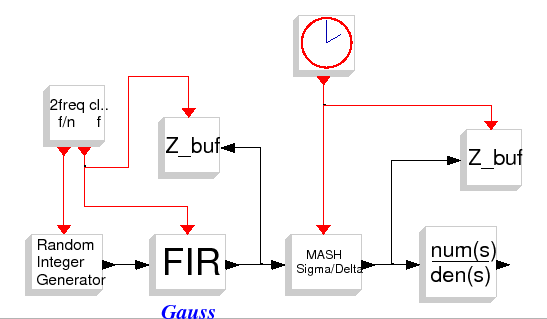
This simulation script enables the analysis of the output spectrum of a $\Delta-\Sigma$ modulator when the modulator works with a gaussian filtered input symbol.

Scicos diagram(s)

$\epsfig{file=dsm_gauss_sim.eps,height=7cm}$

dsm_gauss_sim.cos

Context file(s)

scs_m.props.context=[
'M=1 '
'Te=1'
'Nech=12'
'order=3'
'Tsym=Te*Nech'
'Nsampl=500'
'Tsampl=Tsym/Nsampl'
'fc=0.03*(1/Tsampl)'
'eps=0.7'
'tau=1/(2*%pi*fc)'
'Nsav=2^16'
'Tfin=Nsav*Tsampl'
];

dsm_gauss_sim_ctxt.sce

Used blocks

Simulation script(s)

//Define simulation name
sim_name='dsm_gauss_sim';
sim_path='dsm_gauss_sim';
//Load scicos diagram
load(MODNUMCOS+'/examples/simu/'+sim_path+'/'+sim_name+'.cos');
//Define context
exec(MODNUMCOS+'/examples/simu/'+sim_path+'/'+sim_name+'_ctxt.sce');
context=scs_m.props("context");execstr(context);
//Define Simulation end time
scs_m.props.tf=Tfin;
//Define other variables

for nb_r=1:3
  //substitue context variable to be sweep
  scs_m.props.context=subst_ctxt(scs_m,'order=','order='+string(nb_r));
  //Initialise Info and %scicos_context variable
  Info=list();
  if exists('%scicos_context')==0 then %scicos_context=struct(); end
  //Do simulation with scicos_simulate
  Info=scicos_simulate(scs_m,Info,%scicos_context,"nw");
  //Load result
  myvar=return_state_block(Info,"z_buf");
  if nb_r==1  then
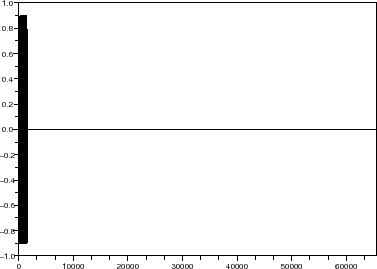
    //draw time domain wave form of gaussian filtered input signal
    scf(10);
    myvart=myvar(1)(1:Nsav);
    plot2d(0:Nsav-1,myvart,rect=[0 -1 Nsav-1 1]);
    //compute fft of gaussian input signal
    DSP1=1/Nsav*abs(fftshift(fft(myvart,-1))^2);
    DSP1_log=10*log10(DSP1(Nsav/2:Nsav));
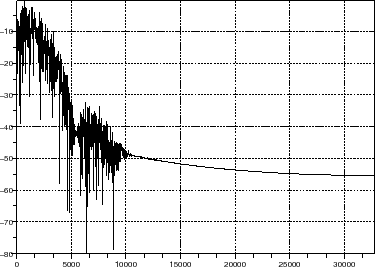
    //draw output sprectrum of gaussian filtered input signal
    scf(20);
    plot2d(0:Nsav/2,DSP1_log,rect=[0 min(DSP1_log) Nsav/2 max(DSP1_log)]);xgrid();
  end
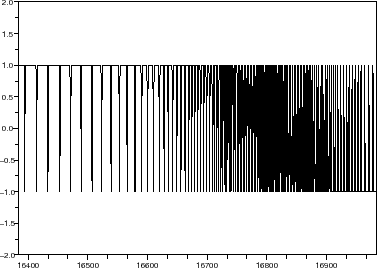
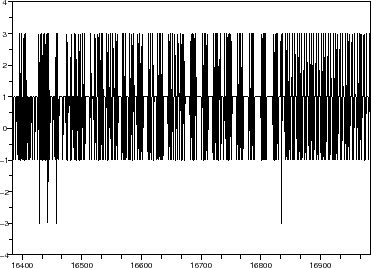
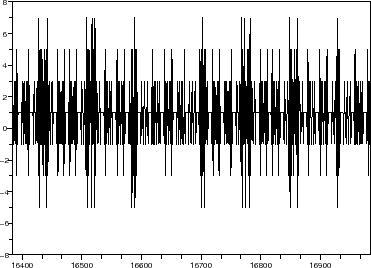
  //draw time domain wave form of sigma-delta modulator output
  scf(10+nb_r);
  plot2d(Nsav/4:Nsav/4+600,myvar(2)(Nsav/4:Nsav/4+600),rect=[Nsav/4 -2^nb_r Nsav/4+600 2^nb_r]);
  //compute fft of sigma-delta modulator output
  myvart=myvar(2)(1:Nsav);
  DSP2=1/Nsav*abs(fftshift(fft(myvart,-1))^2);
  DSP2_log=10*log10(DSP2(Nsav/2:Nsav));
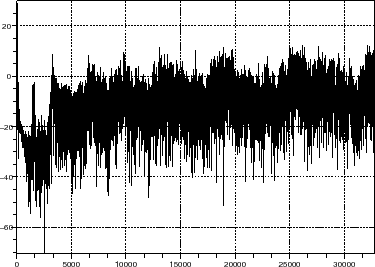
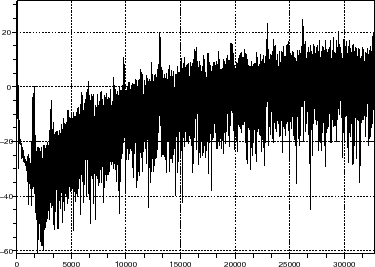
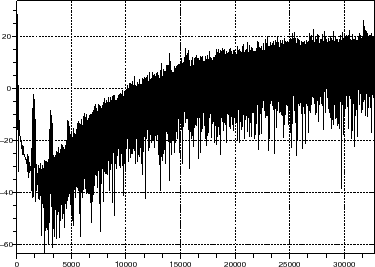
  //draw output sprectrum of sigma-delta modulator
  scf(20+nb_r);
  plot2d(0:Nsav/2,DSP2_log,rect=[0 min(DSP2_log) Nsav/2 max(DSP2_log)]);xgrid();
end

dsm_gauss_sim.sce

Scope results

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_1.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (a) Time domain waveform of gaussian filtered input signal

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_2.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (b) Spectrum of gaussian filtered input signal

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_3.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (c) Time domain output waveform of first order $\Sigma$ - $\Delta$ modulator

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_4.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (d) Spectrum of output waveform of first order $\Sigma$ - $\Delta$ modulator

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_5.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (e) Time domain output waveform of second order $\Sigma$ - $\Delta$ modulator

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_6.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (f) Spectrum of output waveform of second order $\Sigma$ - $\Delta$ modulator

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_7.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (g) Time domain output waveform of third order $\Sigma$ - $\Delta$ modulator

$\begin{figure}\begin{center} \epsfig{file=dsm_gauss_sim_scope_8.eps,width=300.00pt} \end{center}\end{figure}$

Figure : (h) Spectrum of output waveform of third order $\Sigma$ - $\Delta$ modulator

Authors

A. Layec