Scicos Diagram
fr - eng

Second order Infinite Impulse Response filter

Module

• Modnum

Contents

• Second order Infinite Impulse Response filter
  • Module
  • Description
  • Context
  • Scope Results
  • Used blocks
  • See Also
  • Authors
  • Bibliography

Description

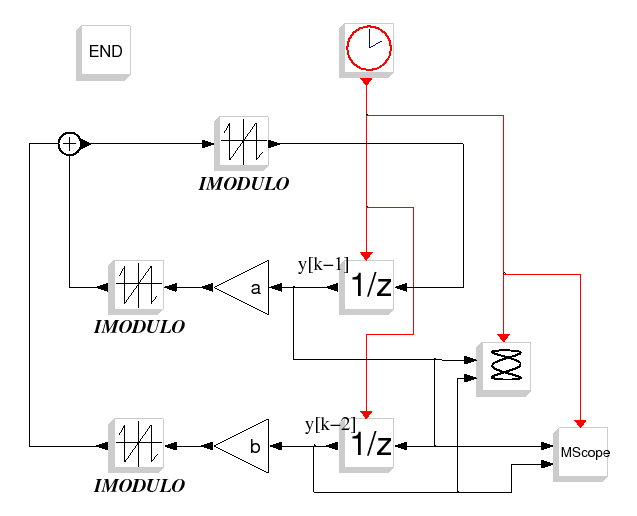
The Fig. 1 presents the block diagram of an ideal second order digital filter.

Figure 1: Block diagram of a linear second order digital recursive filter

The differential discrete equation that described the system is given by:

$$\begin{eqnarray} y\left(z\right)=y\left(z\right)\left(az^{-1}+bz^{-2}\right)+x\left(z\right). \end{eqnarray}$$

This linear system is traditionally studed by the following Z function transfert :

$$\begin{eqnarray} H\left(z\right)=\dfrac{y\left(z\right)}{x\left(z\right)}=\dfrac{1}{1+az^{-1}+bz^{-2}}. \end{eqnarray}$$

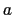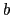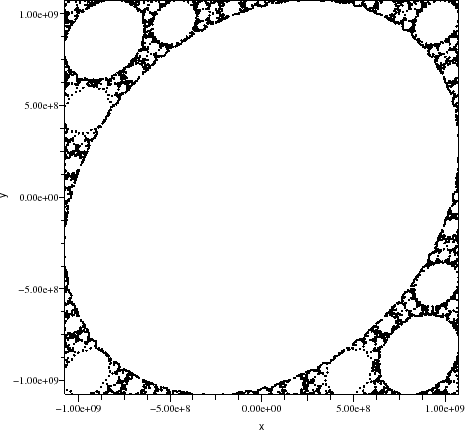
With this previous equation, we can find the stability domain of the filter according to the gain paramaters $a$ and $b$. So the Fig.2 represents the stability domain of the second order recursive filter.

Figure 2: Stability domain of the second order recursive filter

By changing the ideal operators (adders and multipliers) by real operators that are presents in Digital Signal Processors (DSP), we can associate a nonlinear function for each operators. It is the modulo function which represents the effect of the overflow that occurs in digital implementation.

The system is then described by the following nonlinear discrete state system :

$$\begin{eqnarray} y_{1_{k}} & = & F\left(F\left(F\left(ay_{1_{k-1}}\right)+F\left... ...}+x_{k}\right),\nonumber\\ y_{2_{k}} & = & y_{1_{k-1}},\nonumber \end{eqnarray}$$

which is the simulated system in this scicos diagram.

Context

Te     = 1
Nbit   = 31
a      = 0.5
b      = -1
ci     = 0.675
Intmax = 2^(Nbit-1);
ci1    = -int(ci*Intmax)
ci2    = int(ci*Intmax)
Tfin   = 1e4*Te

Scope Results

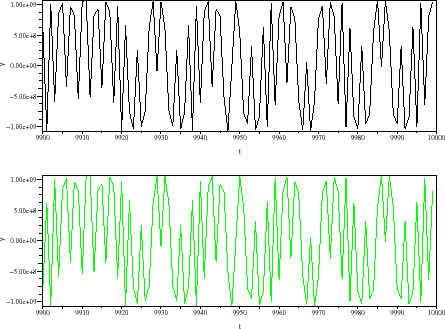
Figure : (a) Time domain waveforms of discrete state variables

Figure : (b) Phase plan

Used blocks

• IMODULO_f - Integer modulo function block

See Also

• lin_chua_cod_decod - Master-slave synchronization of second order IIR filter (Scicos Diagram)
• lin_chua_sim - Output probability density of autonomous second order IIR filter (Scilab simulation Script)
• lin_chua_teb_sim - BER estimation of pair chaotic encoder/decoder with introduction of jitter in receiver clock (Scilab simulation Script)

Authors

A. Layec

Bibliography

[1] L. O. Chua and T. Lin, ``Chaos in digital filters,'' IEEE Trans. Circuits Syst., vol. 35, no. 6, pp. 648-658, Juin 1988.

[2] T. Lin and L. O. Chua, ``On chaos of digital filters in the real world,'' IEEE Trans. Circuits Syst., vol. 38, no. 5, pp. 557-558, Mai 1991.