Discrete zero crossing block
This block realizes a discrete threshold detection, by analyzing instaneous angular position of oscillator and generates events when a crossing at zero occurs.
To understand the computational function of that block, define an oscillator with the following formula :
with 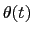 defined by :
defined by :
where 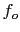 is the free-running frequency and
is the free-running frequency and
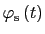 the instantaneous phase of the oscillator. Moreover in steady state assume that :
the instantaneous phase of the oscillator. Moreover in steady state assume that :
When sampling the angular position with constant step, 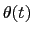 becomes
becomes
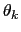 and the following figure can be used to compute the event dates of the oscillator when zero crossing occurs.
and the following figure can be used to compute the event dates of the oscillator when zero crossing occurs.
Figure 1: Discrete computation of zero crossing dates of oscillator
At the time 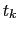 , we can do an extrapolation of the argument of the cosine function by writting the following equality :
, we can do an extrapolation of the argument of the cosine function by writting the following equality :
Finally, we can write the date of the event generation :
with 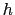 the integration step.
the integration step.
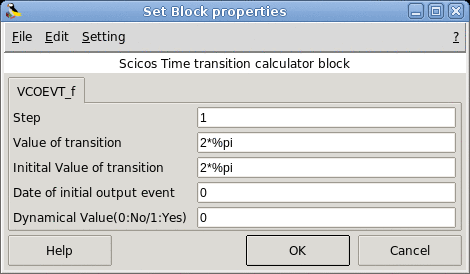
- Step
The time domain integration step.
Properties : Type 'vec' of size 1.
- Value of transition
The angular position to detect for event generation.
Properties : Type 'vec' of size 1.
- Initital Value of transition
The initial value of angular position where the detection begins.
Properties : Type 'vec' of size 1.
- Date of initial output event
The first event date.
Properties : Type 'vec' of size 1.
- Dynamical Value(0:No/1:Yes)
Enable second regular input port that corresponds to the dynamical factor value of the frequency divider.
The position to detect will be multiplied by the value provided by this second input port.
Properties : Type 'vec' of size 1.
- always active: no
- direct-feedthrough: yes
- zero-crossing: no
- mode: no
- regular inputs:
- port 1 : size [1,1] / type 1
- number/sizes of activation inputs: 1
- number/sizes of activation outputs: 1
- continuous-time state: no
- discrete-time state: yes
- object discrete-time state: no
- name of computational function: vcoevt
- MODNUMCOS/macros/scicos_blocks/Pll/VCOEVT_f.sci [view code]
A. Layec
- [1]
A. Demir, ``Analysis and simulation of noise in nonlinear electronic circuits
and system,'' Ph.D., University of California, Berkeley, 1997.


![]()
![]()
![]()
![]() , we can do an extrapolation of the argument of the cosine function by writting the following equality :
, we can do an extrapolation of the argument of the cosine function by writting the following equality :
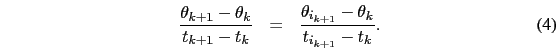
![]()